На практике часто встречается необходимость проведения опытов, для обработки результатов которых применяется геометрическая вероятность
Пусть у нас есть некоторая область G, площадью Sg. Подбрасываем бесконечно маленький шарик. Какова вероятность того что этот шарик попадет в маленькую область g. Предполагается, что наш шарик может попасть в любую точку фигуры, причем вероятность попадания в любую точку фигуры пропорциональна площади этой фигуры, но не зависит от формы, аналогично можно сказать и про маленькую фигуру. Заметим что вместимость G > g во столько же раз во сколько ее площадь больше. Тк все случаи попадания шарика во все точки равновероятны, то рассматриваем вероятность попадания в маленькую фигуру это отношение g/G.
Вывод: В общем случае фигуры которые мы рассматриваем могут иметь разную меру, поэтому мы должны составить отношение мер
Задача о встрече: Два человека условились встретиться в определенном месте между 12 и 13 часами. Пришедший первым ждет второго в течении 20 минут, после чего уходит. Чему равна вероятность встречи этих героев, если приход каждого из них в течении часа может произойти в течении любого момента времени.
Решение:
Из условия задачи ясно, что для выполнения встречи героев, истинным должно быть условие |t1t2|<=20
t1-t2 =20; t1>t2
=20; t1< t2
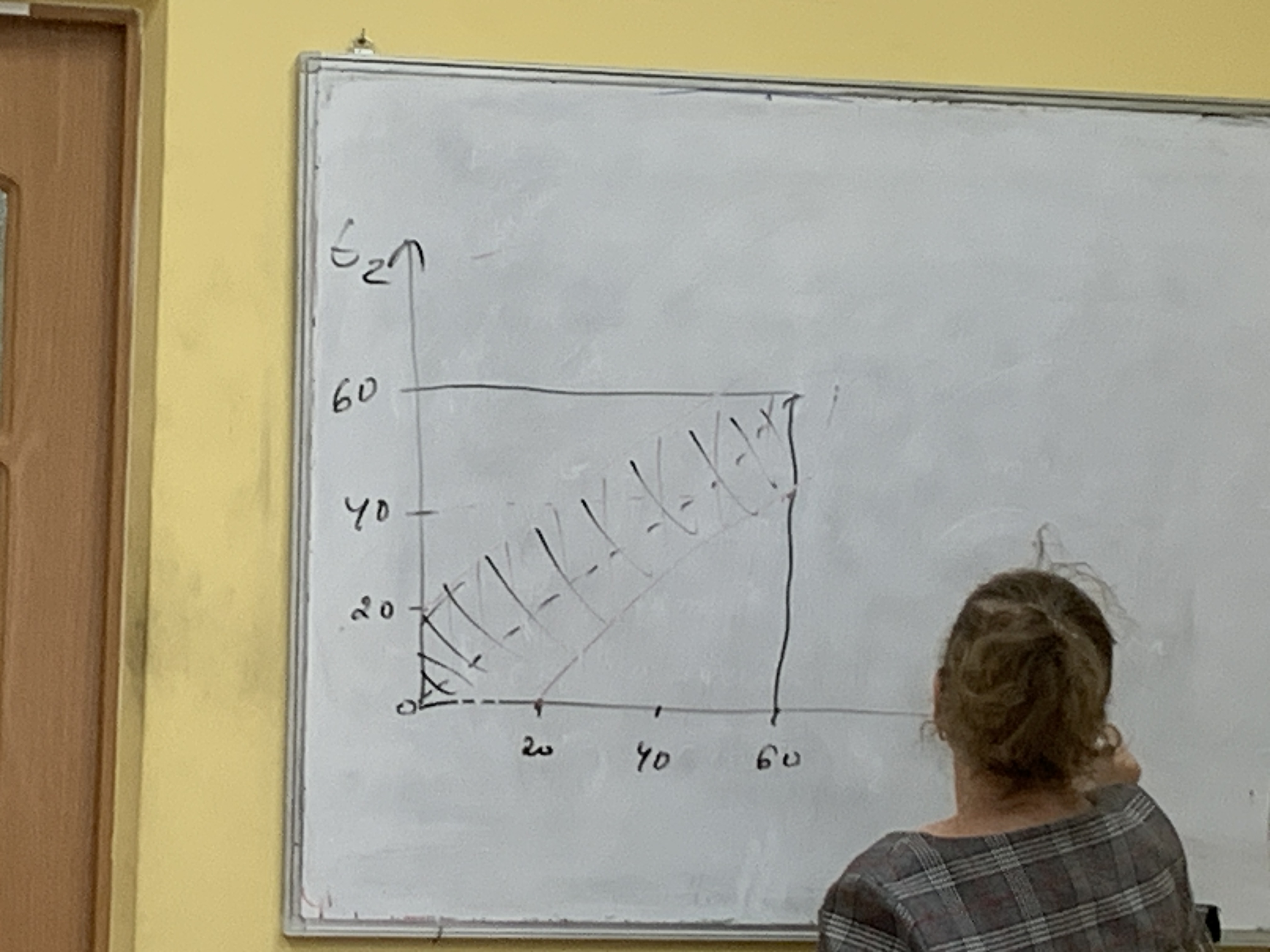
При построении в качестве использования единицы масштаба мы выбираем минуты, тогда всевозможные исходы будут являться точками большого квадрата.
Все исходы благоприятны все исходы в заштрихованной области. События что люди встретятся P(c)=S0/S=60^2 -2^40^2 /2/60=5/9
На практике бывает часто необходимо вычислять вероятность некоторого события A1 которое зависит от B1. Тогда речь идет об условной вероятности для события A1. Поэтому условная вероятность для А1 P(A1/A2)условнаяA1 = P(A1A2)совместная/P(A2)безусловная
Два события называются зависимыми, если вероятность одного события зависит от того произошло ли второе событие или нет.
В нашем случае A1 зависит от A2. Если такая зависимость есть, тогда условная вероятность по своей величине не совпадает с вероятностью события безусловного A1.
Рассматриваемое событие может зависит не только от одного события, но на самом деле может быть и больше. Если событие A2 благоприятствует A1, то условная вероятность должна вот не меньше безусловной вероятности для события A1
Если а1 а2 независимы то справедливо соотношение P(A1/A2)=P(A2).
Если события А1 и А2 независимы то и для обратных событий будет справедливо тоже самое.
Задача:
В урне 10 белых и 5 черных шаров. Из нее последовательно извлекаются два шарика, причем первый вытянутый шар снова возвращается в урну. Пусть А - появление белого шарика при первом извлечении. B - появление белого при втором извлечении.
Решение:
P(A) = 10/15
P(B) = 10/15
События A B - независимые те B не зависит от произошедшего события A.
Р(-А)=5/15
Р(В/А)=Р(В)=10/15
Пусть первый шар не возвращается в урну, тогда В зависит от А.
Р(В/А)=10-1/15-1=9/14
Пусть вероятность события В зависит от -А
Р(В/-А)=10/14
Видим что условная вероятность В меньше чем безусловная В.
При решении подобных задач исходим из особенностей рассматриваемого явления.
Основные законы и формулы теории вероятности
Теорема умножения вероятности. Качается вычисления вероятности произведения двух и большего числа событий: Р(АВ) = Р(А)Р(В/А)=Р(В)Р(А/В)
Безусловные вероятности еще называются оприорными
Условные еще называются апосториорными
Теорема сложения. Касается суммы двух или более событий. P(A+B) = P(A) + P(B) -P(AB)
Обобщенным случаем этой теоремы является ситуация когда событий больше чем два P(A+B+C) = P(A) +P(B)+P(C) - PAB - PBC - PAC + PABC
случайные величины и их классификации
Сл.в - в результате опыта может принимать значение, заранее неизвестное
Сл.в - функция, отображающая пространства элементарных событий на множество чисел, т.е. это числовая функция, аргументом которой является исход случайного опыта. Для случайной величины можно указать только значения одно из которых оно примет в результате опыта, а все перечисленные значения являются возможными.
Contents
Случаные величины большими
Возмодные значения обозначаем малыми буквами
Дискретные случайные величины - может принимать конечное или бесконечное счетные множество значений.
Дискретная случайная величина называется решетчетой, если все возможные значения представляют собой арифметическую прогрессию. Т.е. существуют такие числа А и Х что можем рассчитать дискретное значения xi= a+ ih
Непрерывная Сл в - та , значения котораой непрерывно заполняет некоторый интервал числовой оси. Возможные значения не отделимы друг от друга, но их количество бесконечно .
Смешанного типа - та величина, которая в целом ведет себя непрерывно но может принимать отдельные дискретные значения
Т.е. Одновременно для этой величины мы задаем ее дискретное описание и используем описание для непрерывной
способы описания Сл в
Описывать можно с помощью закона распределения
ЗР(закон распределения) вероятности Сл в - называется всякое соотношение, устанавливающее связь между возможными значениями Сл в и их вероятностями. Т.е. это способ распределения полной вероятности между отдельными ее значениями или группами ее значений.
В качестве ЗР используют ряд, функцию распределения, плотность вероятности, характеристическая функция.
Именно ЗР закон распределения является полным описанием случайной величины
На практике достаточно часто ЗР может быть неизвестен, тогда используют числовые характеристики Сл в. А они являются более сжатым способом описания и только существенные свойства показывают…
Ряд распределения и формы его задания
… (empty)

Возможные значения случайной величины составляют полную группу.